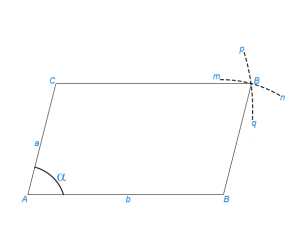
Решение всяких треугольников в конечном счете сводится к решению прямоугольных треугольников. В прямоугольном же треугольнике АВС отношение двух его сторон, например катета а к гипотенузе с, всецело зависит от величины одного из острых углов, например А (рис. 1).
Отношения различных пар сторон прямоугольного треугольника и называются тригонометрическими функциями его острого угла. По отношению к углу А эти функции получают следующие названия и обозначения:1. Синус: sin А = a/c (отношение противолежащего катета к гипотенузе).
2. Косинус: cos А = b/c (отношение прилежащего катета к гипотенузе).
3. Тангенс: tg A = a/b (отношение противолежащего катета к прилежащему).
4. Котангенс: ctg А = b/a (отношение прилежащего катета к противолежащему).
5. Секанс: sec А = c/b (отношение гипотенузы к прилежащему катету).
6. Косеканс: cosec А = c/a (отношение гипотенузы к противолежащему катету).
По отношению к углу В («дополнительному» углу но отношению к А) названия соответственно меняются:
sin В = b/c ; cos В = a/c ; tg В = b/a ;
ctg В = a/b ; sec В = c/a ; cosec В = c/b .
Для некоторых углов можно написать точные выражения их тригонометрических величин. Важнейшие случаи даны в таблице ниже*.
Эта таблица имеет больше теоретическое, чем практическое значение, так как содержит неизвлекаемые точно корни. Для большинства же углов даже и с помощью корней нельзя записать точные числовые значения тригонометрических функций. Но приближенные их значения можно вычислить с любой желаемой степенью точности (см. §26).
| A | sin A | cos A | tg A | ctg A | sec A | cosec A |
| 0° | 0 | 1 | 0 | ∞ | 1 | ∞ |
| 30° | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45° | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 90° | 1 | 0 | ∞ | 0 | ∞ | 1 |
*Углы 0° и 90°, строго говоря, не могут входить в прямоугольный треугольник в качестве его острых углов. Однако при расширении понятия тригонометрической функции (см. §6) рассматриваются значения тригонометрических функций и для этих углов. С другой стороны, один из острых углов треугольника может сколь угодно приблизиться к 90°, другой будет тогда приближаться к нулю; тогда соответствующие тригонометрические величины будут приближаться к значениям, указанным в таблице.
Знак ∞, встречающийся в этой таблице, указывает на то, что абсолютное значение данной величины неограниченно возрастает, когда угол приближается к тому значению, которое указано в таблице. Это и имеют в виду, когда говорят, что величина «равняется бесконечности» или «обращается в бесконечность» (см. Арифметика, §23 и Функции и графики, §12).