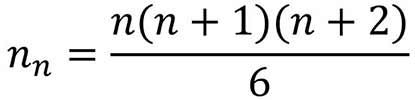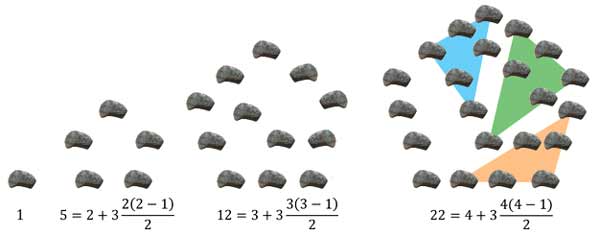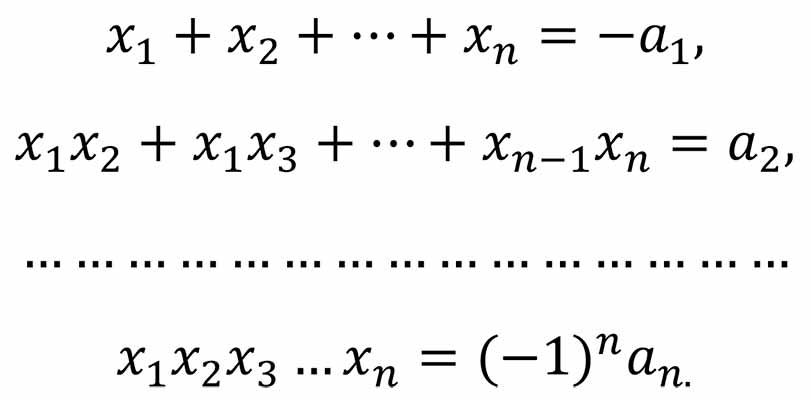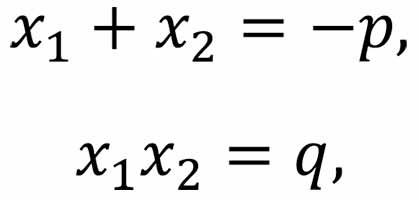Про числа 25, 49, 100 говорят, что они являются квадратами. А почему? Потому что они получаются, если возвести числа 5, 7 и 10 в квадрат. Но имеет ли это название какое-нибудь отношение к геометрической фигуре-квадрату? Посмотрим на рис. 1. Солдаты стоят правильными рядами, образуя квадраты. Число солдат внутри такого квадрата легко подсчитать – нужно умножить их число вдоль горизонтальной стороны на число солдат вдоль вертикальной стороны (заметим, что эти числа равны), и получится общее количество солдат внутри квадрата.
В древности вычислители часто считали с помощью камешков и, естественно, отмечали случаи, когда камешки можно было сложить в виде правильной фигуры. Кроме квадратных чисел были известны треугольные числа, которые получаются так, как это показано на рис. 2.
Нетрудно заметить, что n-е квадратное число равно n2, а n-е треугольное число равно сумме всех целых чисел от 1 до n, т.е.
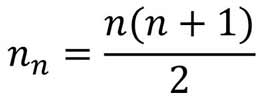
Пятиугольные числа изображены на рис. 3.
Чтобы сосчитать n-е пятиугольное число, его нужно разбить на три треугольных, после чего останется еще n точек, как показано на рисунке. В результате получаем, что n-е пятиугольное число равно
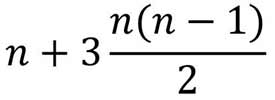
Подобным образом можно образовывать любые многоугольные числа. Формула для n-го k-угольного числа такова:
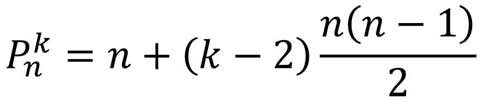
При k = 3 мы получаем треугольные числа, при k = 4 – квадратные и т.д.
Аналогично можно представить число в виде прямоугольника. Для числа 12 это можно сделать многими способами (рис.4), а для числа 13-лишь расположив все предметы в одну линию. Такое число древние не считали прямоугольным. Таким образом, прямоугольными числами являются все составные числа, а непрямоугольными – простые числа.

Рис.4
К фигурным числам также относятся пирамидальные числа, которые получаются, если шарики складывать пирамидой, как раньше складывали ядра около пушки. Нетрудно заметить, что n-е пирамидальное число равно сумме всех треугольных чисел-от первого до n-го. Формула для вычисления n-го пирамидального числа имеет вид