Что такое многочлен
Многочленом Р(х) от одной переменной х называют выражение вида
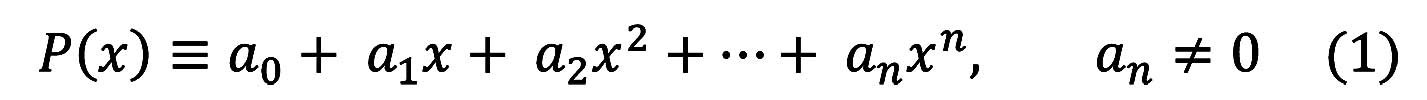
Число n называют степенью многочлена, аn – старшим коэффициентом, а0-свободным членом.
Сложение и умножение многочлена
Для многочленов определены операции сложения и умножения по правилам:
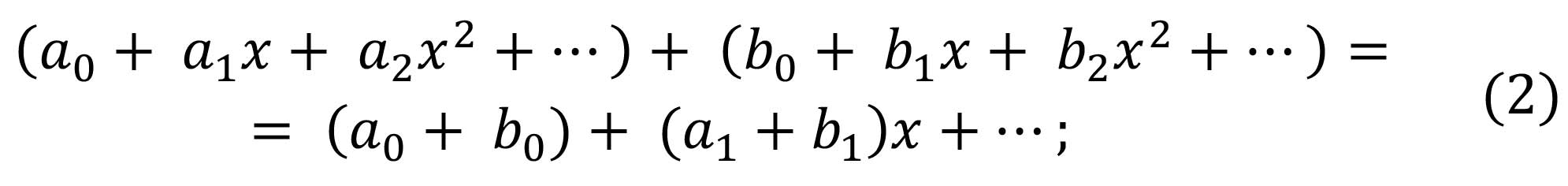
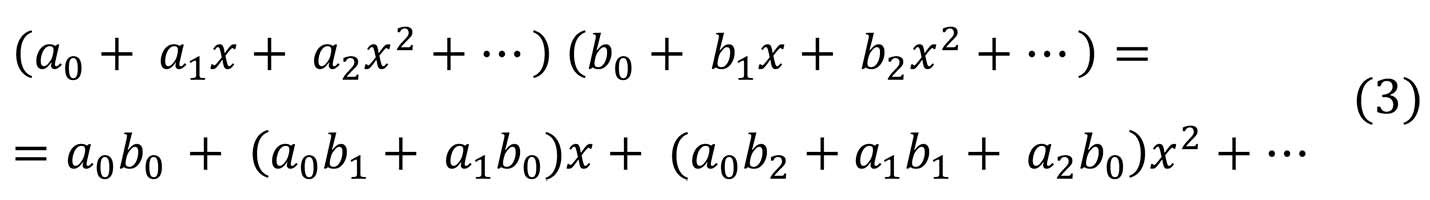
Нетрудно проверить, что свойства операций НаД многочленами аналогичны свойствам арифметических операций над действительными числами:
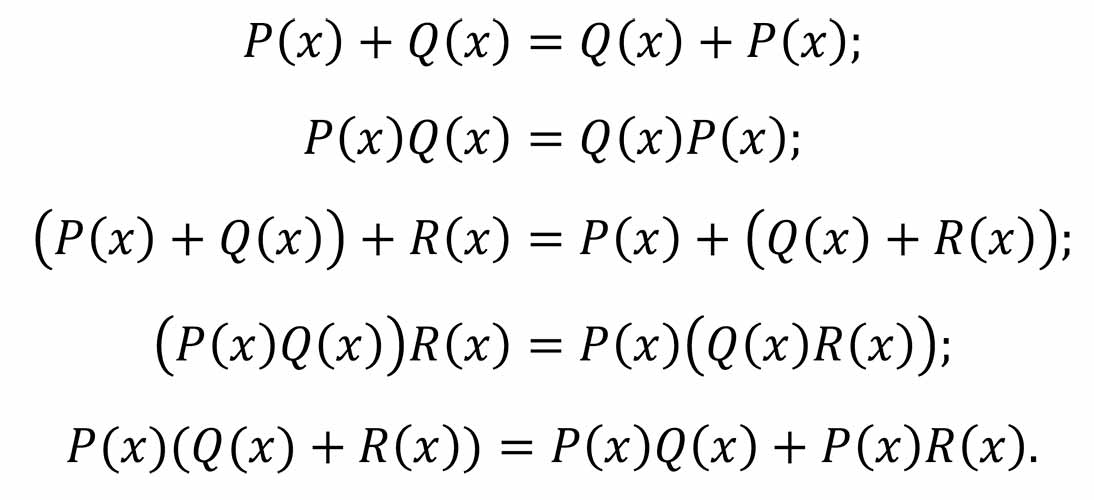
Уравнение вида Р(х) = 0, где Р(х)-многочлен и-й степени от х, называют алгебраическим уравнением n-й степени. Число х0, такое, что Р (х0) = 0, называют корнем многочлена.
Основные теорема алгебры многочленов
В 1799 г. немецкий математик К.Ф. Гаусс доказал теорему, которая носит название «основная теорема алгебры многочленов»: любой многочлен ненулевой степени с комплексными коэффициентами имеет хотя бы один комплексный корень.
В конце XVIII в. французский математик Э. Безу сформулировал и доказал следующую теорему: остаток от деления многочлена Р(х) (с действительными коэффициентами) на двучлен х – а равен Р (а). Отсюда, в частноти получается, что если а-корень многочлена Р, то Р(х) делится без остатка на х – а. Наибольшая степень к такая, что многочлен Р(х) делится на (х – а)к, называется кратностью корня а. Так как при делении многочлена степени n на двучлен х – а получается многочлен степени n – 1, то с учетом основной теоремы алгебры приходим к выводу: многочлен степени n (с комплексными коэффициентами) имеет в точности n корней, если каждый корень считать столько раз, какова его кратность. Кроме того, этот многочлен можно разложить на линейные множители:
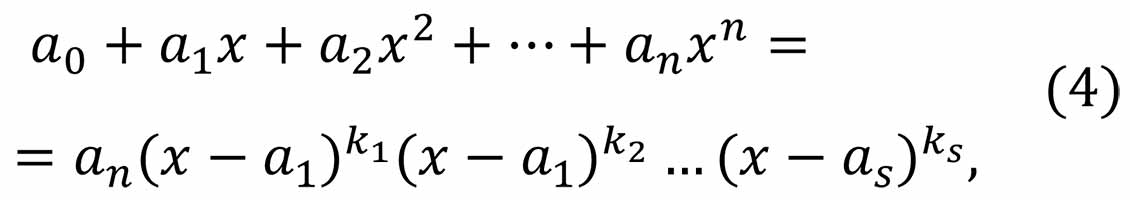
где а1, а2, …, аs – корни многочлена, k1 + к2 + + … + ks = n, ki,-кратность корня аi. Можно доказать, что если a + bi-корень многочлена с действительными коэффициентами, то и а – bi – также его корень. Перемножая в разложении (4) множители (х – а – bi) и (х – а + bi), получим многочлен второй степени с действительными коэффициентами: (х – а – bi) (х – а + bi) = (х – а)2 + b2.
Отсюда следует, что многочлен с действительными коэффициентами можно разложить на множители первой и второй степени с действительными коэффициентами.
Французский математик Ф. Виет (1540-1603) установил следующие соотношения между корнями x1, x2, …, xn уравнения
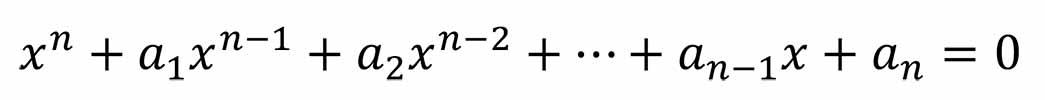
и его коэффициентами:
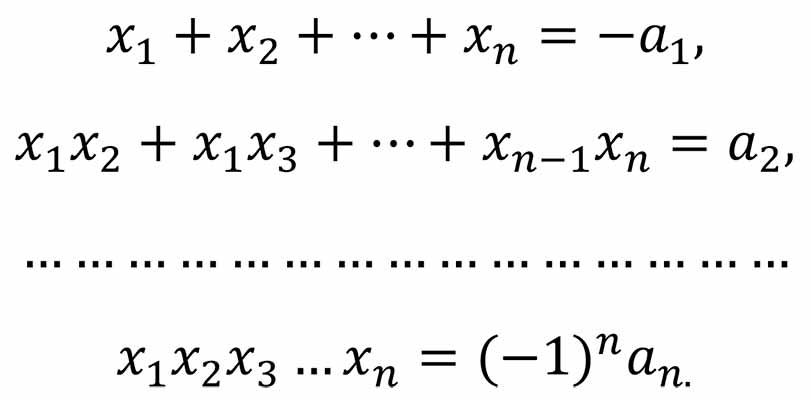
Это утверждение называется теоремой Виета. Для квадратного трехчлена х2 + рх + q соотношения имеют вид
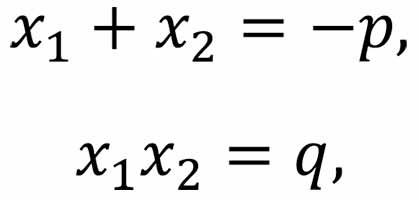
где x1 и x2 – корни трехчлена.
Велика роль многочленов в математике. Многочлены являются довольно простыми функциями. Их легко дифференцировать и интегрировать. Оказывается, любую непрерывную функцию на заданном отрезке можно сколь угодно хорошо приблизить многочленом, например так, чтобы их значения отличались меньше чем на 0,001. Приближение функции многочленом в небольшой окрестности некоторой точки определения функции позволяет выяснить характер поведения функции вблизи этой точки: возрастает или убывает функция, или в этой точке она имеет экстремум (см. Экстремум функции).
Большой вклад в теорию приближения функций многочленами внес П.Л.Чебышев.