На сторонах прямого ушла ВАС (рис.1) откладываем равные отрезки АВ и АС и соединяем их концы отрезком прямой СВ. Прямая ВС образует с АС и АВ углы под 45°
Архив за месяц: Сентябрь 2014
§ 8. Построить углы 60° и 30°
Из концов А и В (рис.1) произвольного отрезка АВ описываем дуги радиусом АВ. Точки их пересечения С и D соединяем прямой, которая пересечет отрезок АВ в середине О. Точку А соединяем отрезком прямой с точкой С. ∠САО=60°, ∠АСО=30°
§ 7. При данной вершине K и луче KM построить угол, равный данному углу ABC
Из вершины В описываем дугу PQ произвольного радиуса (рис.1). Тем же раствором циркуля описываем из центра К дугу pq. Из точки р засекаем дугу ab радиусом, равным PQ. Точку q пересечения дуг pq и ab соединяем с К. Угол qKM искомый.
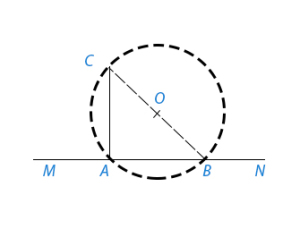
§ 6. Опустить перпендикуляр из данной точки С на прямую MN
Из точки С проводим наклонную СВ (рис.1); находим ее середину О (см. §2) из нее описываем окружность радиусом ОВ. Окружность пересекает MN еще в точке А. Проведя АС, получим искомый перпендикуляр.
В случае, когда точка С лежит близко к прямой MN, этот способ может дать большую погрешность. Тогда лучше пользоваться следующим построением. Из точки С, как из центра (рис.2), проводим дугу DE произвольного радиуса, пересекающую MN в точке D, E. Из точек D, E, как из центров, проводим одним и тем же радиусом две дуги cd, ab, пересекающиеся в точке F. Проведя прямую через точки F и С, получи искомый перпендикуляр.
§ 5. Восстановить перпендикуляр к прямой MN в данной ее точке А
§ 1. Предмет алгебры
Предметом алгебры является изучение уравнений и ряда вопросов, которые развились из теории уравнений. В настоящее время, когда математика разделилась на ряд специальных областей, к области алгебры относят лишь уравнения определенного типа, так называемые алгебраические уравнения.
§ 3. Отрицательные числа
На самых ранних ступенях развития люди знали только натуральные числа. Но этими числами нельзя обойтись даже в самых простых случаях жизни. Действительно, одно натуральное число невозможно в общем случае разделить на другое, если пользоваться только натуральными числами. Между тем в жизни нужно бывает делить, скажем, 3 на 4, 5 на 12 и так далее. Без введения дробных чисел деление натуральных чисел есть невозможное действие; введение дробей делает это действие возможным.
Но действие вычитания и после введения дробей остается не всегда возможным: нельзя вычесть большее число из меньшего, например 5 из 3. Однако в повседневной жизни и не представляется необходимым производить подобное вычитание, и потому очень долгое время оно считалось не только невозможным, но и совершенно бессмысленным.
Развитие алгебры показало, что такое действие необходимо ввести в математику, и оно было узаконено индийскими учеными примерно в 7 в. п. э., а китайскими еще раньше. Индийские ученые, стараясь найти и в жизни образцы такого вычитания, пришли к толкованию его с точки зрения торговых расчетов. Если купец имеет 5000 руб. и закупает товара на 3000 руб., у него остается 5000 – 3000 = 2000 руб. Если же он имеет 3000 руб., а закупает на 5000 руб., то он остается в долгу на 2000 руб. В соответствии с этим считали, что здесь совершается вычитание 3000 – 5000, результатом же является число 2000 (2000 с точкой наверху), означающее «две тысячи долга».
Толкование это носило искусственный характер, купец никогда не находил сумму долга вычитанием 3000 – 5000, а всегда выполнял вычитание 5000 – 3000. Кроме того, на этой основе можно было с натяжкой объяснить лишь правила сложения и вычитания «чисел с точками», но никак нельзя было объяснить правила умножения или деления. Все же толкование это долго приводилось в учебниках и в некоторых книгах приводится и поныне.
«Невозможность» вычитания большего числа из меньшего обусловливается тем, что натуральный ряд чисел бесконечен только в одну сторону. Если последовательно вычитать 1, начиная, скажем, из числа 7, мы получим числа
6, 5, 4, 3, 2, 1,
дальнейшее вычитание дает уже «отсутствие числа», а дальше не из чего уже вычитать. Если же мы хотим сделать вычитание всегда возможным, мы должны:
1) «отсутствие числа» считать также числом (нуль);
2) от этого последнего числа считать возможным отнять еще единицу и т. д.
Так мы получаем новые числа, обозначаемые в настоящее время так:
-1, -2, -3 и т. д.
Эти числа называются целыми отрицательными числами. Стоящий впереди знак «минус» напоминает о происхождении отрицательного числа из последовательного вычитания единицы. Знак этот называется «знаком количества» в отличие от знака вычитания, имеющего ту же форму; последний называется «знаком действия».
Введение целых отрицательных чисел влечет за собой введение и дробных отрицательных чисел. Если мы принимаем, что
0 – 5 = 5,
то должны принять также, что
0 – 12/7 = -12/7
Число -12/7 есть дробное отрицательное число.
В противоположность отрицательным числам (целым и дробным) те числа (целые и дробные), которые рассматриваются в арифметике, называются положительными. Чтобы еще более оттенить эту противоположность, положительные числа снабжаются часто знаком «плюс», который в этом случае есть знак количества (а не знак действий).
Например,
число 2 записывают +2.
Отрицательные и положительные числа, взятые вместе, в школьных руководствах именуют относительными числами.
В принятой научной терминологии эти числа вместе с числом нуль называют рациональными. Смысл этого названия выясняется при введении понятия иррационального числа.
Подобно тому как до введения отрицательного числа нет никаких положительных чисел и число 3/4 есть просто дробное число, а не положительное дробное число, так и до введения иррационального числа +5, -5, -3/4, +3/4 и т.д. просто суть положительные и отрицательные целые и дробные числа, а не рациональные числа.
§ 31. Проценты
Процентом (от латинского pro cento – с сотни) называется сотая часть.
Запись 1% означает 0,01; 27% = 0,27; 100% = 1; 150% =1,5 и т. д. ). 1% от зарплаты означает 0,01 зарплаты; выполнить весь план – значит выполнить 100% плана; выполнение 150% плана означает выполнение 1,5 плана и т. д.*
Чтобы найти процентное выражение данного числа, нужно умножить это число на 100 (или, что то же, перенести в нем запятую через два знака вправо).
Примеры. Процентное выражение числа 2 есть 200 %; числа 0,357 есть 35,7%, числа 1,753 есть 175,3%.
Чтобы найти число по его процентному выражению, нужно разделить процентное выражение на 100 (или, что то же, перенести запятую через два знака влево).
Примеры. 13,5% = 0,135; 2,3% = 0,023; 145 % = 1,45; 2/5 % = 0,4% = 0,004.
Три основные задачи на проценты таковы:
1. Найти указанный процент данного числа. Данное число помножается на число процентов, результат делится на 100 (или, переносится через два знака влево).**
Пример 1. По плану суточная добыча шахты должна равняться 2860 тоннам угля. Шахта приняла обязательство выполнять 115 % плана. Сколько тонн угля должна дать шахта в сутки?
Решение.
1) 2860*115 = 328900.
2) 328900:100 = 3289 т ***
2. Найти число по данной величине указанного его процента. Данная величина делится на число процентов; результат умножается на 100 (т. е. запятая переносится через два знака вправо)****.
Пример 2. Вес сахарного песка составляет 12,5% от веса переработанной свекловицы. Сколько свекловицы требуется для изготовления 3000 ц сахарного песка?
Решение.
1) 3000:12,5 = 240.
2) 240*100 = 24000 (ц)*****.
3. Найти выражение одного числа в процентах другого. Умножаем первое число на 100; результат делим на второе число.
Пример 3. Метод скоростного обжига кирпича, предложенный мастером П. А. Дувановым, позволил ему, увеличить выпуск кирпича с одного кубического метра печи с 1200 до 2300 штук. На сколько процентов увеличилось при этом производство кирпича?
Решение.
1) 2300 – 1200 = 1100,
2) 1100 * 100 = 110000,
3) 110000 : 1200 = 91,67.
Производство кирпича увеличилось на 91, 67 %.
Пример 4. За 1 квартал 2030 г. В России выпущено промышленной продукции на 18 783,6 млн. руб., а за I квартал 2031 г. на 21 500,1 млн. руб. Какой процент составляет продукция I квартала 2031 г. к продукции I квартала 2030 г.?
Решение.
1) 21500,1*100 = 2 150 010.
2) 2 150 010; 18783,6 ≈ 114,5.
Продукция I квартала 2007 г. составляет 114,5 % продукции I квартала 2006 г.
Замечание 1. Во всех трех задачах можно менять порядок действий, например, в последней задаче сначала выполнить деление, а затем результат помножить на 100.
Замечание 2. Нижеприведенный пример предостережет читателя от следующей часто делаемой ошибки.
Пусть требуется узнать, сколько стоил метр ткани до снижения цен, если после понижения продажной цены на 15 % эта ткань продается по 120 руб. за метр. Иногда находят 15% от 120 руб., т. е. помножают 120 * 0,15 = 18. Затем складывают 120 +18 = 138 и считают, что старая цена была 138 руб. за метр. Это неверно, так как процент снижения устанавливается по отношению к прежним ценам, а 18 руб. составляет от 138 руб. не 150 %, а около 13% .
Правильное решение таково: после снижения цен стоимость ткани составила 100% – 15% = 85% от прежней цены. Поэтому прежняя цена (см. задачу 2) составляла 120 : 0,85 = 141,18 руб. за метр.
Замечание 3. При всех вычислениях с процентами. На практике следует пользоваться способами приближенных вычислений.
*Обозначение % произошло от искажения записи cto (сокращение слова cento)
**Иными словами, данное число помножается на дробь, выражающую указанный процент.
***Описанное действие равносильно следующему: 2860 * 1,15 = 3289
****Иными словами, данная величина делится на дробь, выражающую указанный процент.
*****Описанное действие равносильно следующему: 3000:0,125 = 24000.
§ 13. Общий наибольший делитель
Общим делителем нескольких чисел называется число, служащее делителем для каждого из них.
Например, числа 12, 18, 30 имеют общий делитель 3; число 2 – тоже их общий делитель. Среди всех общих делителей всегда имеется наибольший, в нашем примере – число 6. Это число называется Общим Наибольшим Делителем (О.Н.Д.).
Примеры.
Для чисел 16, 20, 28 О.Н.Д. есть 4;
для чисел 5, 30, 60, 90 О.Н.Д. есть 5.
Когда числа небольшие, их О.Н.Д. легко находится по догадке. Если мы имеем дело с большими числами, разлагаем каждое на простые множители и выписываем те из них, которые входят во все данные числа. Каждый из таких множителей берем с наименьшим показателем, с которым он входит в данные числа. Производим умножение.
Пример 1.
Найти О.Н.Д. чисел 252, 441, 1080.
Разлагаем на простые множители
252 = 2²*3²*7;
441=3²*7²;
1080=2³*3³*5
Общим для чисел является только простой множитель 3; наименьший из показателей, с которыми он входит в данные числа, есть 2, О.Н.Д. равен 3³=9
Пример 2.
Найти О.Н.Д. чисел 234, 1080, 8100.
234 = 2*3²*13;
1080 = 2³*3³*5;
8100 = 2²*3*3³*5²;
О.Н.Д. = 2*3²= 18.
Может случиться, что простых множителей, общих для всех данных чисел, не будет вовсе. Тогда общий наибольший делитель есть 1. Например, для чисел 15 = 3*5, 10 = 2*5, 6 = 2*3 О.Н.Д. = 1. Два числа, О.Н.Д. которых равен 1, называются взаимно простыми. Например, 15 и 22 – взаимно простые числа.
§ 32. О приближенных вычислениях
Числа, с которыми мы имеем дело в жизни, бывают двух родов. Одни в точности дают истинную величину, другие – только приблизительно. Первые называют точными, вторые – приближенными. Часто мы сознательно берем приближенное число вместо точного, так как последние нам не требуется. Во многих же случаях точное число невозможно найти по сути дела.
Пример 1. В книге 412 страниц; число 412 – точное.
Пример 2. В шестиугольнике 9 диагоналей; число 9 – точное.
Пример 3. Продавец свесил на автоматических весах 50 г масла. Число 50 – приближенное, так как весы нечувствительны к увеличению или уменьшению веса на 0,5 г.
Пример 4. Расстояние от ст. Москва до ст. С.Петербург Октябрьской ж. д. составляет 651 км. Число 651 – приближенное, так как, с одной стороны, наши измерительные инструменты неточны, с другой же стороны, сами станции имеют некоторое протяжение.
Результат действий с приближенными числами есть тоже приближенное число. При этом неточными могут оказаться и те цифры, которые получены действиями над точными цифрами данных чисел.
Пример 5. Перемножаются приближенные числа 60,2 и 80,1. Известно, что все выписанные цифры верны, так что истинные величины могут отличаться от приближенных лишь сотыми, тысячными и т. д. долями. В произведении получаем 4822,02. Здесь могут быть неверными не только цифры сотых и десятых, но и цифры единиц. Пусть, например, сомножители получены округлением точных чисел 60,25 и 80,14. Тогда точное произведение будет 4828,435, так что цифра единиц в приближенном произведении (2) отличается от точной цифры (8) на 6 единиц.
Теория приближенных вычислений позволяет:
1) зная степень точности данных, оценить степень точности результатов еще до выполнения действий;
2) брать данные с надлежащей степенью точности, достаточной, чтобы обеспечить требуемую точность результата, но не слишком большой, чтобы избавить вычислителя от бесполезных расчетов;
3) рационализировать самый процесс вычисления, освободив его от тех выкладок, к которые не окажут влияния на точные цифры результата.