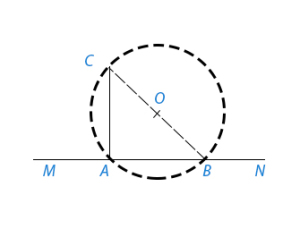
Из точки С проводим наклонную СВ (рис.1); находим ее середину О (см. §2) из нее описываем окружность радиусом ОВ. Окружность пересекает MN еще в точке А. Проведя АС, получим искомый перпендикуляр.
В случае, когда точка С лежит близко к прямой MN, этот способ может дать большую погрешность. Тогда лучше пользоваться следующим построением. Из точки С, как из центра (рис.2), проводим дугу DE произвольного радиуса, пересекающую MN в точке D, E. Из точек D, E, как из центров, проводим одним и тем же радиусом две дуги cd, ab, пересекающиеся в точке F. Проведя прямую через точки F и С, получи искомый перпендикуляр.