Архив за месяц: Сентябрь 2014

§ 12. Предел

Добавить комментарий

Постоянная величина а называется пределом переменной величины х, если эта переменная при своем измерении неограниченно приближается к а*.

Существенно иметь в виду, что при рассмотрении самой по себе взятой переменной величины не может быть речи о нахождении ее предела. Если же рассматриваются две переменные величины и одна есть функция другой, то для одной из них (аргумента) можно задать предел, а для другой — искать его (если он существует).

Пример 1. Переменные х, у связаны зависимостью у=(x2-4)/(x-2); наити предел у, когда х имеет пределом число 6.

Будем неограниченно приближать переменную х к числу 6 каким-либо способом; например, будем давать х значения 6,1; 6,01; 6,001 и т.д.; мы найдем для у значения 8,1; 8,01, 8,001 и т.д.; эти значения неограниченно приближаются к числу 8. То же окажется, если х неограниченно приближать к числу 6 любым другим способом, например полагать х = 5,9; 6,01; 5,999; 6,0001 и т.д. Поэтому, когда х имеет пределом 6, у имеет пределом 8.
Запись:

lim y=8
x→6

или

lim (x2-4)/(x-2)=8
x→6

Обозначение lim представляет сокращение французского слова limite (лимит), означающего “предел”. Полученный результат в данном случае мы могли бы найти, подставив x=6 в выражении y=(x2-4)/(x-2). В следующем примере этот способ не приводит к успеху.

Пример 2. Дано y=(x2-4)/(x-2). Найти lim y. Подставив х=2 в выражение (x2-4)/(x-2), найдем неопределенное выражение 0/0 (II, §23). Между тем вычисления, подобные проделанным в примере 1, покажут, что

Этот результат можно было бы получить и так:
имеем

§ 3. Обратная функция

Добавить комментарий

Для характеристики функции совершенно не существенно, какой буквой обозначается сама функция и ее аргумент; так, если имеем у=х2 и u=v2, то у есть такая же функция х, как и функция v; иначе говоря, х2 и v2  — это одна и та же функция, хотя аргумент ее обозначен неодинаково.

Если в данной функциональной зависимости аргумент и функцию поменять ролями, мы получаем новую функцию, называемую обратной по отношению к исходной.

Пример 1. Пусть имеем функцию и аргумента v

u=v2

Если поменять ролями аргумент и функцию, величина v будет функцией u и представится формулой v=√u . Если аргумент в обоих случаях обозначить одной и той же буквой х, то исходная функция есть х2, а обратная ей √x.

Пример 2. Функцией, обратной sin х, является arcsin х. Действительно, если у=sin х, то х=arcsin у (V, §24).

О графике обратной функции см.§8, п.7.

§ 2. Функциональная зависимость между двумя переменными

Добавить комментарий

Говорят, что две переменные величины х, у связаны функциональной зависимостью, если каждому значению, которое может принять одна из них, соответствует одно или несколько определенных значений другой.

Пример 1. Температура Т кипения воды и атмосферное давление р связаны функциональной зависимостью, так как каждому значению Т соответствует одно определенное значение р и обратно. Так, если Т = 100°С, то р непременно равно 760 мм рт. ст.; если Т = 70°С, то р = 234 мм рт.ст. и т.д. Напротив, атмосферное давление р и относительная влажность воздуха х (рассматриваемые как переменные величины) не связаны функциональной зависимостью: если известно, что х = 90% , то о величине р нельзя еще сказать ничего определенного.

Пример 2. Площадь равностороннего треугольника S и его периметр р связаны функциональной зависимостью. Формула S = (√3 : 36) р2 представляет эту зависимость.

Если желательно подчеркнуть, что в данном вопросе значения переменной у должны находиться по заданным значениям переменной х, то последняя (х) называется независимой переменной или аргументом, а первая (у) — зависимой переменной или функцией.

Пример 3. Если по величине периметра р равностороннего треугольника мы хотим судить о его площади S (см. пример 2), то р есть аргумент (независимая переменная), a S — функция (зависимая переменная).

Чаще всего независимая переменная обозначается буквой х.

Если каждому значению аргумента х соответствует только одно значение функции у, то функция называется однозначной, если два или более — многозначной (двузначной, трехзначной и т.д.).

Пример 4. Тело брошено вверх; s — высота его подъема над землей; t — время, прошедшее с момента броска. Величина s есть однозначная функция t, так как в каждый данный момент высота тела — вполне определенная величина. Величина t — двузначная функция s, так как тело находится на данной высоте s дважды — один раз при полете вверх, другой раз при падении вниз.

Формула s = v0t – 0,5gt2, связывающая переменные s, t (начальная скорость v0 и ускорение свободного падения g — в данном случае постоянные величины), показывает, что при данном t имеем одно значение s, а при данном s — два значения t, определяемые из квадратного уравнения

0,5gt2 -v0t+s = 0.

§ 1. Постоянные и переменные величины

Добавить комментарий

Применение математики к изучению законов природы и к использованию их в технике заставило ввести в математику понятие переменной величины и, в противоположность ей, понятие постоянной величины. Переменная величина — это такая величина, которая в условиях данного вопроса может принимать различные значения. Постоянная величина в условиях данного вопроса сохраняет неизменное значение. Одна и та же величина в одном вопросе может быть постоянной, в другом — переменной величиной.

Пример. Температура Т кипения воды в большинстве физических вопросов есть величина постоянная (Т = 100 °С). Однако в тех вопросах, где нужно считаться с изменением атмосферного давления, Т есть величина переменная.

Различение постоянных и переменных величин особенно часто применяется в высшей математике; в элементарной математике основную роль играет разделение величин на известные и неизвестные. Последнее сохраняется и в высшей математике, но не играет там основной роли.

Чаще всего переменные величины обозначаются последними буквами латинского алфавита х, у, z,…, а постоянные — первыми а, Ь, с, … .

§ 2. Исторические сведения о развитии тригонометрии

Добавить комментарий

Потребность в решении треугольников раньше всего возникла в астрономии, и в течение долгого времени тригонометрия развивалась и изучалась как один из отделов астрономии.

Насколько известно, способы решения треугольников (сферических) впервые были письменно изложены греческим астрономом Гиппархом в середине 2 века до н.э. Наивысшими достижениями греческая тригонометрия обязана астроному Птолемею (2 век н.э.), создателю геоцентрической системы мира, господствовавшей до Н.Коперника.

Греческие астрономы не знали синусов, косинусов и тангенсов. Вместо таблиц этих величин они употребляли таблицы, позволявшие находить хорду окружности по стягиваемой дуге. Дуги измерялись в градусах и минутах; хорды тоже измерялись градусами (один градус составлял шестидесятую часть радиуса),минутами и секундами. Это шестидесятеричное подразделение греки заимствовали у вавилонян (см.II, §7)

Таблицы, составленные Птолемеем, содержали хорды всех дуг через каждые 1°/2*, вычисленные с точностью до секунды. С помощью интерполяции по ним можно было найти с той же точностью хорду любой дуги. (Для упрощения интерполяции Птолемей дает поправки на 1′.) При вычислении таблиц Птолемей опирался на открытую им теорему о диагоналях вписанного четырехугольника (IV, Б, §19).

Значительной высоты достигла тригонометрия и у индийских средневековых астрономов. Как и греки, индийцы заимствовали вавилонское градусное измерение дуг. Но индийцы рассматривали не хорды дуг, а линии синусов и косинусов (т. е. линии РМ и ОР для дуги AM на рис. 1). Кроме того, рассматривалась линия РА, получившая позднее в Европе название «синус-верзус».

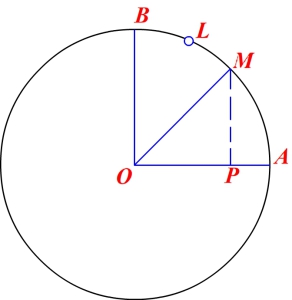
Исторические сведения о развитии тригонометрии

рис. 1

За единицу измерения отрезков МР, ОР, РА принималась дуговая минута. Так, линия синуса дуги АВ = 90° есть ОВ — радиус окружности; дуга AL, равная радиусу, содержит (округленно) 57°18′ = 3438′. Поэтому синус дуги 90° считался равным 3438′.

Дошедшие до нас индийские таблицы синусов (древнейшая составлена в 4—5 веке н. э.) не столь точны, как птолемеевы; они составлены через 3°45′ (т.е. через 1/24 часть дуги квадранта).

Дальнейшее развитие тригонометрия получила в 9—14 веках в трудах арабоязычных авторов. В 10 веке багдадский ученый Мухаммед из Буджана, известный под именем Абу-ль-Вефа, присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов. Он дает им те же определения, которые содержатся в наших учебниках. Абу-ль-Вефа устанавливает также основные соотношения между этими линиями (соответствующие формулам §14). В руках знаменитого мусульманского ученого Насир эд-Дина из Туса (1201 —1274) тригонометрия становится самостоятельной научной дисциплиной. Насир эд-Дин систематически рассматривал все случаи решения плоских и сферических треугольников и указал ряд новых способов решения.

В 12 веке был переведен с арабского языка на латинский ряд астрономических работ, и по ним впервые европейцы познакомились с тригонометрией2. Однако со многими достижениями арабоязычной науки европейцам не удалось познакомиться своевременно. В частности, им осталась неизвестной работа Насир эд-Дина. Выдающийся немецкий астроном 15 века Региомонтан (1436—1476) через 200 лет после Насир эд-Дина заново открыл его теоремы.

Региомонтан составил обширные таблицы синусов (через 1 минуту с точностью до седьмой значащей цифры). Он впервые отступил от шестидесятеричного деления радиуса и за единицу измерения линии синуса принял одну десятимиллионную часть радиуса. Таким образом, синусы выражались целыми числами (а не 60-ричными дробями). До введения десятичных дробей оставался только один шаг. Но он потребовал более 100 лет (см.II, § 31).

За таблицами Региомонтана последовал ряд других, еще более подробных. Друг Коперника Ретик (1514—1576) вместе с несколькими помощниками в течение 30 лет работал над таблицами, законченными и изданными в 1596 г. его учеником Ото. Углы шли через 10″, а радиус делился на 1 ООО ООО ООО ООО ООО частей, так что синусы имели 15 верных цифр!

Буквенные обозначения (в алгебре они появились в конце 16 века) утвердились в тригонометрии лишь в середине 18 века благодаря русскому академику Л.Эйлеру (1707—1783). Этот великий математик придал всей тригонометрии ее современный вид. Величины sin х, cos х и т.д. он рассматривал как функции (VI, § 2) числа х — радианной меры соответствующего угла. Эйлер давал числу х всевозможные значения: положительные, отрицательные и даже комплексные. Он ввел и обратные тригонометрические функции (§24).

*) Если взять центральный угол, опирающийся на половину рассматриваемой дуги, то хорда будет удвоенной линией синуса этого угла. Поэтому таблица Птолемея равносильна пятизначной таблице значений синуса через 1°/4.

2) В это «время появился латинский термин “синус”, что означает «пазуха» или «карман». Это — перевод арабского слова «джейб», имеющего то же значение. Как появился этот арабский термин, неизвестно. Некоторые полагают, что он произошел из индийского (санскритского) слова «жиа» или «жила» (первое значение — тетива; в геометрии — хорда). Но синус в индийской терминологии именуется «ардха-жиа», т. е. полухорда.
Название “косинус” появилось только в начале 17 века как сокращение наименования complementi sinus (синус дополнения), указывающего, что косинус угла А есть синус угла, дополняющего угол А до 90°. Наименования «тангенс» и «секанс» (в переводе с латинского означающие “касательная” и “секущая”) введены в 1583 г. немецким ученым Финком.

§ 1. Предмет тригонометрии

Добавить комментарий

Слово «тригонометрия» искусственно составлено из греческих слов: «тригонон» — треугольник и «метрезис» — измерение (соответствующим русским термином было бы «треугольникомерие»). Основная задача тригонометрии состоит в решении треугольников т. е. в вычислении неизвестных величин треугольника по данным значениям других его величин. Так, в тригонометрии решают задачу о вычислении углов треугольника по данным его сторонам, задачу о вычислении сторон треугольника — по площади и двум углам и т.д. Так как любую вычислительную задачу геометрии можно свести к решению треугольников, то тригонометрия охватывает всю планиметрию и стереометрию и широко применяется во всех областях естествознания и техники.

Учение о решении сферических треугольников называется сферической тригонометрией; в противоположность этому учение о решении обычных треугольников называют плоской или прямолинейной тригонометрией.

Углы произвольного треугольника нельзя связать непосредственно с его сторонами с помощью алгебраических соотношений. Поэтому в тригонометрии вводятся, кроме самих углов, еще новые тригонометрические величины (их перечень и определения см. § 5). Эти величины уже можно связать со сторонами треугольника простыми алгебраическими соотношениями. С другой стороны, по данному углу можно вычислить соответствующее значение тригонометрической величины, и обратно.

Значение каждой тригонометрической величины изменяется с изменением угла, которому она соответствует: другими словами, тригонометрическая величина есть функция угла (VI, § 2). Отсюда наименование: тригонометрические функции.

Между различными тригонометрическими функциями существуют важные зависимости. Использование их позволяет сокращать и облегчать вычисления. Часть тригонометрии, посвященная изучению этих соотношений, называется гониометрией, т.е. “угломерием” («гонйа» — по-гречески «угол»).

§ 1. Общие замечания

Добавить комментарий

Стереометрия изучает геометрические свойства пространственных тел и фигур. При решении геометрических задач важнейшим приемом является рассмотрение плоских линий и фигур как тех, которые непосредственно обнаруживаются в изучаемом предмете, так и тех, которые строятся в качестве вспомогательных. Поэтому очень важно научиться распознавать и выделять в пространственных образах разнообразные плоские фигуры

§ 4. Прямая линия, луч, отрезок

Добавить комментарий

Прямую линию можно мысленно продолжить в обе стороны безгранично. В геометрии название “прямая” обозначает обычно прямую линию, не ограниченную ни с одной, ни с другой стороны. Часть прямой линии, с одной стороны ограниченная, а с другой – нет, называется полупрямой или лучом. Часть прямой линии, ограниченная с обеих сторон, называется отрезком.

§ 3. Теоремы, аксиомы, определения

Добавить комментарий

Рассуждение, устанавливающее, какое-либо свойство, называется доказательством. Доказываемое свойство называется теоремой. При доказательстве геометрической теоремы мы опираемся на ранее установленные свойства. Некоторые из них в свою очередь являются теоремами; некоторые же считаются в геометрии основными и принимаются без доказательства. Свойства, принимаемые без доказательства, называются аксиомами.

Аксиомы возникли из опыта, и опыт же проверяет истинность аксиом в их совокупности. Проверка состоит в том, что все теоремы геометрии согласовываются с опытом; этого не случилось бы, если бы система аксиом была ложной.

Ни одно геометрическое свойство, взятое в отдельности, не является аксиомой, так как его всегда можно доказать на основании других свойств. Так, в геометрии обычно принимается за аксиому следующее свойство параллельных прямых: «через одну и ту же точку нельзя провести две различные прямые, параллельные одной и той же прямой» (аксиома параллельности). На основании этой аксиомы (и ряда других) доказывается такое свойство треугольника: «сумма углов треугольника равна 180°». Между тем мы могли бы последнее свойство принять за аксиому вместо аксиомы параллельности (оставив остальные аксиомы прежними). Тогда упомянутое свойство параллельных прямых можно доказать и оно станет теоремой.

Таким образом, систему аксиом можно выбирать различными способами. Нужно только, чтобы взятых аксиом было достаточно для вывода всех прочих геометрических свойств. В геометрии стремятся число аксиом по возможности уменьшить. Это делается для того, чтобы уяснить логические связи между отдельными свойствами.

Аксиомы предпочтительно выбираются из числа простейших геометрических свойств. Впрочем, по вопросу о простоте того или иного свойства мнения могут быть различны.

Некоторые понятия в геометрии мы принимаем за начальные, их содержание можно выяснить только из опыта (таково, например, понятие точки). Все остальные понятия мы объясняем, опираясь на начальные. Такие объяснения называются определениями. Каждое геометрическое определение опирается либо непосредственно на начальные понятия, либо на понятия, определенные прежде.

Одно и то же геометрическое понятие можно определять различно. Например, диаметр окружности можно определить как хорду, проходящую через центр, или как хорду наибольшей длины. Приняв за определение одно из этих свойств, можно доказать другое. Предпочтительно взять за определение простейшее свойство; впрочем, и здесь невозможно обеспечить всеобщего согласия.

§ 2. Исторические сведения о развитии геометрии

Добавить комментарий

Первые геометрические понятия приобретены людьми в глубокой древности. Они возникли из потребности определять вместимость различных предметов (сосудов, амбаров и т. п.) и площади земельных участков. Древнейшие известные нам письменные памятники, содержащие правила для определения площадей и объемов, были составлены в Египте и Вавилоне около 4 тысяч лет назад. Около 2,5 тысяч лет назад греки заимствовали у египтян и вавилонян их геометрические знания. Первоначально эти знания применялись преимущественно для измерения земельных участков. Отсюда греческое название «геометрия», что означает «землемерие».

Греческие ученые открыли множество геометрических свойств и создали стройную систему геометрических знаний. В ее основу они положили простейшие геометрические свойства, подсказанные опытом. Остальные свойства выводились из простейших с помощью рассуждений.

Эта система около 300 г. до н.э. получила завершенный вид в «Началах» Евклида, где изложены так-же основы теоретической арифметики. Геометрические разделы «Начал» по содержанию и по строгости изложения примерно совпадают с современными школьными учебниками геометрии.

Однако там ничего не говорится ни об объеме, ни о поверхности шара, ни об отношении окружности к диаметру (хотя есть теорема о том, что площади кругов относятся, как квадраты диаметров). Приближенная величина этого отношения была известна из опыта задолго до Евклида, но только в середине 3 века до н.э. Архимед (287—212 гг.) строго доказал, что отношение окружности к диаметру (т.е. число π) заключено между 3(1/7) и 3(10/71). Архимед доказал также, что объем шара меньше объема описанного цилиндра ровно в 1,5 – раза и что поверхность шара в 1,5 раза меньше
полной поверхности описанного цилиндра.

В способах, примененных Архимедом для решения упомянутых задач, содержатся зачатки методов высшей математики. Эти способы Архимед применил к решению многих трудных задач геометрии и механики, очень важных для строительного дела и для мореплавания. В частности, он определил объемы и центры тяжести многих тел и изучил вопрос о равновесии плавающих тел различной формы.

Греческие геометры исследовали свойства многих линий, важных для практики и для теории. Особенно полно они изучили конические сечения. Во втором веке до н. э. Аполлоний обогатил теорию конических сечений многими важными открытиями, остававшимися непревзойденными в течение 18 веков.

Для изучения конических сечений Аполлоний пользовался методом координат. К изучению всевозможных линий на плоскости этот метод был применен лишь в 30-х годах 17 века французскими учеными П.Ферма (1601 – 1655) и Р.Декартом (1596 – 1650). Для технической практики того времени было достаточно плоских линий. Лишь сто лет спустя, когда этого потребовали возросшие запросы астрономии, геодезии и механики, координатный метод был применен к изучению кривых поверхностей и линий, проведенных на кривых поверхностях.

Систематическое развитие метода координат в пространстве было дано русским академиком Л. Эйлером— гениальным и всесторонним ученым.

Более двух тысяч лет система Евклида считалась непреложной. Но в 1826 г. гениальный русский ученый Николай Иванович Лобачевский создал новую геометрическую систему. Исходные ее положения отличаются от основных положений Евклида лишь в одном пункте1. Но отсюда вытекает множество очень существенных особенностей.

Так, в геометрии Лобачевского сумма углов треугольника всегда меньше, чем 180° (в геометрии Евклида она равна 180°). При этом недостаток до 180° тем больше, чем больше площадь треугольника. Может показаться, что опыт опровергает этот и другие выводы Лобачевского. Но это не так. Непосредственно измеряя углы треугольника, мы находим, что они в сумме составляют примерно 180°. Точной же величины суммы мы не можем найти вследствие несовершенства измерительных инструментов. Между тем все те треугольники, которые доступны нашему измерению, слишком малы, чтобы непосредственными измерениями обнаружить недостаток суммы углов до 180°.

При дальнейшем развитии гениальных идей Лобачевского оказалось, что система Евклида недостаточна для исследования многих вопросов астрономии и физики, где мы имеем дело с фигурами огромных размеров. Однако в условиях повседневного опыта она остается вполне пригодной. А так как к тому же она обладает преимуществом простоты, то ее применяют и будут применять в технических расчетах, ее изучают и будут изучать в школах.

1 В геометрии Евклида через точку А проходит только одна прямая, лежащая в одной плоскости с данной прямой ВС и не пересекающая ее. В геометрии Лобачевского таких прямых бесчисленное множество.