Поступает, как в предыдущей задаче; прямой угол α строим, как в §5
§ 28. Построить прямоугольник по данным сторонам
Добавить комментарий
Архив метки: геометрические построения
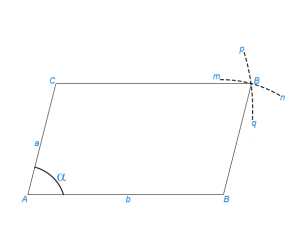
§ 27. Построить параллелограмм по данным сторонам a и b и одному из углов α
Строим ∠ А=α (см. §7); на его сторонах откладываем отрезки АС=а, АВ=b (рис.1). Проводим из В дугу mn радиусом а и из С – дугу pq радиусом b. Точку пересечения этих дуг D соединяем с С и В.
рис.1
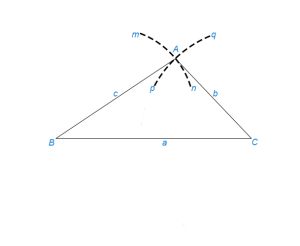
§ 26. Построить треугольник по трем сторонам а, b, с
Пусть наибольшую длину имеет отрезок а. Если а<b+c, то искомый треугольник можно построить так: откладываем отрезок ВС=а (рис.1). Из концов В и С описываем дуги mn и pq радиусами с и b соответственно. Точку пересечения дуг А соединяем с В и С. Если a>b+c, то задача не имеет решения. В промежуточном случае а=b+c условию отвечает только “вырожденный треугольник” – все его вершины лежат на одной прямой.
рис.1
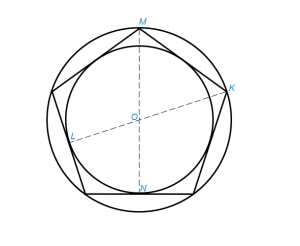
§ 25. Вписать окружность в данный правильный многоугольник
Центр окружности находится, как в предыдущем параграфе §24. Из центра опускаем перпендикуляр ON на одну из сторон (рис.1). Радиусом ON (или OL, рис.2) описываем окружность.
рис.1
рис.2
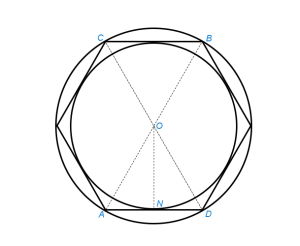
§ 24. Описать окружность около данного правильного многоугольника
Если число сторон четно (рис.1), соединяем прямыми АВ и CD две любые пары противоположных вершин. Из точки их пересечения О радиусом ОА описываем окружность.
рис.1
Если число сторон нечетно (рис.2), опускаем из двух любых вершин К и М перпендикулярны KL и MN на противоположные стороны. Из точки их пересечения О радиусом ОК описываем окружность.
рис.2
§ 23. Вписать окружность в ромб (или квадрат) ABCD
Из точки О пересечения диагоналей проводим ОЕ ⊥ АВ (рис.1). Окружность с центром О и радиусом ОЕ – искомая.
рис.1
В неравносторонний параллелограмм вписать окружность нельзя.
§ 22. Описать окружность около данного прямоугольника (квадрата) ABCD
Проводим диагонали BD и AC (рис.1). Из точки О их пересечения проводим окружность радиусом ОА.
рис.1
Около косоугольного параллелограмма описать окружность нельзя.
§ 21. Вписать окружность в данный треугольник АВС
Делим пополам два угла треугольника (рис.1), например А и С. Из точки О пересечения биссектрис проводим OD ⊥ AC (см. §6). Радиусом OD описываем искомую окружность.
рис.1
§ 19. Провести к двум данным окружностям общую внутреннюю касательную
Задача не имеет решения, если один из кругов лежит внутри другого, а также если данные круги пересекаются. В случае внешнего касания (рис.1) задача имеет одно решение: через точку М проводим KL ⊥ AB.
рис.1
В остальных случаях имеем два решения (DE и D’E’ рис.2). Из центра А проводим окружность радиусом, равным сумме радиусов данных окружностей. Из центра В проводим касательную ВС к построенной окружности (§17). Точку касания С и центра А соединяем отрезком АС, который пересечет окружность (А) в точке D. Из В проводим радиус ВЕ ⊥ ВС. Конец его Е соединяем с D; ED – искомая касательная. Так же строится и другая касательная E’D’.
рис.2
§ 18. Провести к данным двум окружностям общую внешнюю касательную
а) Если радиусы данных окружностей равны между собой, задача всегда имеет два решения (рис.1). Через центры А и В проводим диаметры КК’ и LL’, получаем искомые решения.
рис.1
б) Пусть радиусы данных окружностей не равны: R > r; из центра большого круга проводим окружность радиусом AC=R – r (рис.2). К ней проводим касательную ВС из центра В меньшего круга (см. §17). Центр А соединяем с точкой касания С прямой. Продолжаем ее и получаем на большей окружности точку D.
рис.2
Проводим ВЕ перпендикулярно к ВС до пересечения в точке Е с меньшей окружностью. Через точку D и Е проводим прямую. Прямая DE – искомая касательная. Задача допускает два решения (DE и D’E’), если меньший круг не лежит целиком внутри большего. Если меньший круг лежит внутри большего (рис.3) , задача не имеет решений.
рис.3
В промежуточном случае, когда окружности имеют внутреннее касание (рис.4), задача имеет одно решение: через точку внутреннего касания М проводим KL ⊥ AM
рис.41