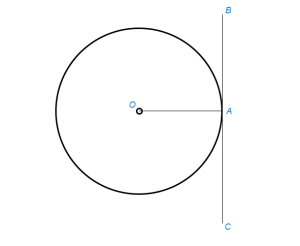
Задача не имеет решения, если один из кругов лежит внутри другого, а также если данные круги пересекаются. В случае внешнего касания (рис.1) задача имеет одно решение: через точку М проводим KL ⊥ AB.

рис.1

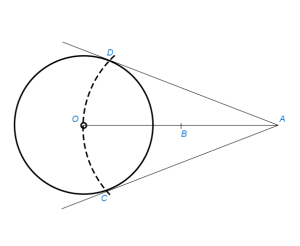
В остальных случаях имеем два решения (DE и D’E’ рис.2). Из центра А проводим окружность радиусом, равным сумме радиусов данных окружностей. Из центра В проводим касательную ВС к построенной окружности (§17). Точку касания С и центра А соединяем отрезком АС, который пересечет окружность (А) в точке D. Из В проводим радиус ВЕ ⊥ ВС. Конец его Е соединяем с D; ED – искомая касательная. Так же строится и другая касательная E’D’.

рис.2

а) Если радиусы данных окружностей равны между собой, задача всегда имеет два решения (рис.1). Через центры А и В проводим диаметры КК’ и LL’, получаем искомые решения.

рис.1

б) Пусть радиусы данных окружностей не равны: R > r; из центра большого круга проводим окружность радиусом AC=R – r (рис.2). К ней проводим касательную ВС из центра В меньшего круга (см. §17). Центр А соединяем с точкой касания С прямой. Продолжаем ее и получаем на большей окружности точку D.

рис.2

Проводим ВЕ перпендикулярно к ВС до пересечения в точке Е с меньшей окружностью. Через точку D и Е проводим прямую. Прямая DE – искомая касательная. Задача допускает два решения (DE и D’E’), если меньший круг не лежит целиком внутри большего. Если меньший круг лежит внутри большего (рис.3) , задача не имеет решений.

рис.3

В промежуточном случае, когда окружности имеют внутреннее касание (рис.4), задача имеет одно решение: через точку внутреннего касания М проводим KL ⊥ AM

рис.41

Если точка А лежит на окружности (рис.1), строим ВАС перпендикулярно к радиусу ОА (см. §5); ВС – искомая касательная.

рис.1

Если А лежит вне круга (рис.2), делим АО пополам (см. §2) и из середины В проводим радиусом ВО дугу CD. Точки D и С соединяем прямыми с А. Прямые AD и AC – искомые касательные.

рис.2