Архив метки: окружность

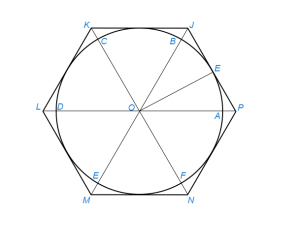
§ 37. Около данного круга описать правильные треугольник, пятиугольник, шестиугольник, восьмиугольник, десятиугольник

Добавить комментарий

Отметим на окружности (рис.1) вершины A, B, …, F правильного вписанного многоугольника с тем же числом сторон (см. §33 и §36). Проведем радиусы ОА, ОВ, …, OF и продолжим их. Дугу АВ разделим пополам точкой Е (см. §15). Через Е проведем JP⊥OE. Отрезок JP, заключенный между продолжениями соседних радиусов, есть сторона искомой фигуры. На продолжении остальных радиусов откладываем отрезки ОК, OL, …, ON, равные OP. Точки J, K, L, …, N, P последовательно соединяем. Многоугольник JKLM…NP – искомый.

Около данного круга описать правильные треугольник, пятиугольник, шестиугольник, восьмиугольник, десятиугольник

рис.1

§ 36. Вписать правильный десятиугольник в данный круг

Добавить комментарий

Построим точку F (рис.1), как и в §33 OF есть сторона искомой фигуры. Раствором циркуля, равным OF, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры

Вписать правильный десятиугольник в данный круг

рис.1

§ 35. Вписать правильный восьмиугольник в данный круг

Добавить комментарий

Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Разделив пополам дуги AD, DB, BC, CA точками E, F, G, H (см. §15), последовательно соединяем полученные восемь точек.

Вписать правильный восьмиугольник в данный круг

рис.1

§ 33. Вписать правильный пятиугольник в данный круг

1 комментарий

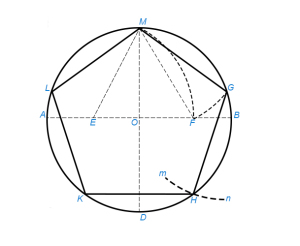
Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Делим пополам радиус АО точкой Е. Из Е радиусом ЕС проводим дугу CF, пересекая ее диаметр АВ в точке F. Из С радиусом CF проводим дугу FG, пересекая ею данную окружность в точке G; CG(=CF) есть одна сторона искомой фигуры. Проводим тем же радиусом дугу mn из точки П как из центра, получаем еще одну вершину H искомой фигуры и т.д.

Вписать правильный пятиугольник в данный круг

рис.1

§ 32. Описать квадрат около данного круга

Добавить комментарий

Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Из их концов, как из центров, описываем четыре полуокружности радиусами, равными ОА. Точки F, G, H и E их пересечения – вершины искомого квадрата.

Описать квадрат около данного круга

рис.1

§ 31. Вписать квадрат в данный круг

1 комментарий

Проводим два взаимно перпендикулярных диаметра АВ и СD; ACBD – искомый квадрат (рис.1)

Вписать квадрат в данный круг

рис.1

§ 25. Вписать окружность в данный правильный многоугольник

Добавить комментарий

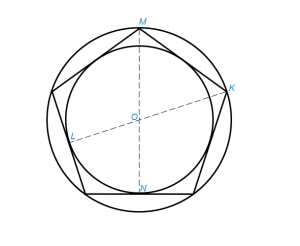
Центр окружности находится, как в предыдущем параграфе §24. Из центра опускаем перпендикуляр ON на одну из сторон (рис.1). Радиусом ON (или OL, рис.2) описываем окружность.

Описать окружность около данного правильного многоугольника

рис.1

Описать окружность около данного правильного многоугольника

рис.2

§ 24. Описать окружность около данного правильного многоугольника

Добавить комментарий

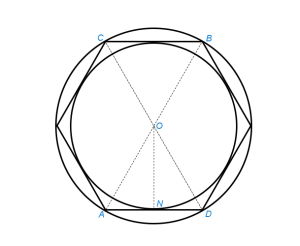
Если число сторон четно (рис.1), соединяем прямыми АВ и CD две любые пары противоположных вершин. Из точки их пересечения О радиусом ОА описываем окружность.

Описать окружность около данного правильного многоугольника

рис.1

Если число сторон нечетно (рис.2), опускаем из двух любых вершин К и М перпендикулярны KL и MN на противоположные стороны. Из точки их пересечения О радиусом ОК описываем окружность.

Описать окружность около данного правильного многоугольника

рис.2

§ 23. Вписать окружность в ромб (или квадрат) ABCD

Добавить комментарий

Из точки О пересечения диагоналей проводим ОЕ ⊥ АВ (рис.1). Окружность с центром О и радиусом ОЕ – искомая.

Вписать окружность в ромб (или квадрат)

рис.1

В неравносторонний параллелограмм вписать окружность нельзя.

§ 22. Описать окружность около данного прямоугольника (квадрата) ABCD

Добавить комментарий

Проводим диагонали BD и AC (рис.1). Из точки О их пересечения проводим окружность радиусом ОА.

Описать окружность около данного прямоугольника (квадрата)

рис.1

Около косоугольного параллелограмма описать окружность нельзя.