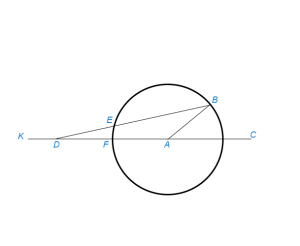
Простой линейкой и циркулем точно выполнить это построение нельзя. С помощью циркуля и сантиметровой линейки построение можно выполнить так (рис.1): произвольным радиусом АС описываем из точки А окружность. Продолжаем АС за точку А. Кладем линейку так, чтобы она проходила через точку В, и вращаем ее вокруг В до тех пор, пока отрезок ED между окружностью и прямой АК не станет равным радиусу АС. Тогда угол EDF есть треть угла ВАС.
рис.1
Из вершины A проводим дугу DE произвольным радиусом (рис.1). Из точек D и Е ее пересечения со сторонами АВ и АС описываем произвольными равными радиусами (удобнее всего прежним раствором циркуля) дуги ab, ac. Точку их пересечения соединяем с А; полученная прямая AF делит угол ВАС пополам
рис.1
На сторонах прямого ушла ВАС (рис.1) откладываем равные отрезки АВ и АС и соединяем их концы отрезком прямой СВ. Прямая ВС образует с АС и АВ углы под 45°
рис.1
Из концов А и В (рис.1) произвольного отрезка АВ описываем дуги радиусом АВ. Точки их пересечения С и D соединяем прямой, которая пересечет отрезок АВ в середине О. Точку А соединяем отрезком прямой с точкой С. ∠САО=60°, ∠АСО=30°
рис.1
Из вершины В описываем дугу PQ произвольного радиуса (рис.1). Тем же раствором циркуля описываем из центра К дугу pq. Из точки р засекаем дугу ab радиусом, равным PQ. Точку q пересечения дуг pq и ab соединяем с К. Угол qKM искомый.
рис.1
Из точки С проводим наклонную СВ (рис.1); находим ее середину О (см. §2) из нее описываем окружность радиусом ОВ. Окружность пересекает MN еще в точке А. Проведя АС, получим искомый перпендикуляр.
рис.1
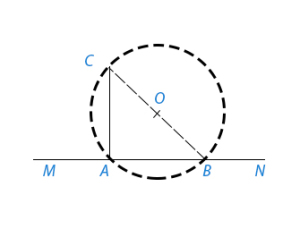
В случае, когда точка С лежит близко к прямой MN, этот способ может дать большую погрешность. Тогда лучше пользоваться следующим построением. Из точки С, как из центра (рис.2), проводим дугу DE произвольного радиуса, пересекающую MN в точке D, E. Из точек D, E, как из центров, проводим одним и тем же радиусом две дуги cd, ab, пересекающиеся в точке F. Проведя прямую через точки F и С, получи искомый перпендикуляр.
рис.2
Взяв произвольную точку О вне данной прямой (рис.1), проводим из нее окружность радиусом ОА. Через вторую точку В пересечения окружности с прямой MN проводим диаметр ВС; конец диаметра С соединяем с А; СА – искомый перпендикуляр
рис.1
Стереометрия изучает геометрические свойства пространственных тел и фигур. При решении геометрических задач важнейшим приемом является рассмотрение плоских линий и фигур как тех, которые непосредственно обнаруживаются в изучаемом предмете, так и тех, которые строятся в качестве вспомогательных. Поэтому очень важно научиться распознавать и выделять в пространственных образах разнообразные плоские фигуры
Прямую линию можно мысленно продолжить в обе стороны безгранично. В геометрии название “прямая” обозначает обычно прямую линию, не ограниченную ни с одной, ни с другой стороны. Часть прямой линии, с одной стороны ограниченная, а с другой – нет, называется полупрямой или лучом. Часть прямой линии, ограниченная с обеих сторон, называется отрезком.
Рассуждение, устанавливающее, какое-либо свойство, называется доказательством. Доказываемое свойство называется теоремой. При доказательстве геометрической теоремы мы опираемся на ранее установленные свойства. Некоторые из них в свою очередь являются теоремами; некоторые же считаются в геометрии основными и принимаются без доказательства. Свойства, принимаемые без доказательства, называются аксиомами.
Аксиомы возникли из опыта, и опыт же проверяет истинность аксиом в их совокупности. Проверка состоит в том, что все теоремы геометрии согласовываются с опытом; этого не случилось бы, если бы система аксиом была ложной.
Ни одно геометрическое свойство, взятое в отдельности, не является аксиомой, так как его всегда можно доказать на основании других свойств. Так, в геометрии обычно принимается за аксиому следующее свойство параллельных прямых: «через одну и ту же точку нельзя провести две различные прямые, параллельные одной и той же прямой» (аксиома параллельности). На основании этой аксиомы (и ряда других) доказывается такое свойство треугольника: «сумма углов треугольника равна 180°». Между тем мы могли бы последнее свойство принять за аксиому вместо аксиомы параллельности (оставив остальные аксиомы прежними). Тогда упомянутое свойство параллельных прямых можно доказать и оно станет теоремой.
Таким образом, систему аксиом можно выбирать различными способами. Нужно только, чтобы взятых аксиом было достаточно для вывода всех прочих геометрических свойств. В геометрии стремятся число аксиом по возможности уменьшить. Это делается для того, чтобы уяснить логические связи между отдельными свойствами.
Аксиомы предпочтительно выбираются из числа простейших геометрических свойств. Впрочем, по вопросу о простоте того или иного свойства мнения могут быть различны.
Некоторые понятия в геометрии мы принимаем за начальные, их содержание можно выяснить только из опыта (таково, например, понятие точки). Все остальные понятия мы объясняем, опираясь на начальные. Такие объяснения называются определениями. Каждое геометрическое определение опирается либо непосредственно на начальные понятия, либо на понятия, определенные прежде.
Одно и то же геометрическое понятие можно определять различно. Например, диаметр окружности можно определить как хорду, проходящую через центр, или как хорду наибольшей длины. Приняв за определение одно из этих свойств, можно доказать другое. Предпочтительно взять за определение простейшее свойство; впрочем, и здесь невозможно обеспечить всеобщего согласия.