Проводим два взаимно перпендикулярных диаметра АВ и СD; ACBD – искомый квадрат (рис.1)
рис.1
§ 31. Вписать квадрат в данный круг
1 комментарий
Архив рубрики: Геометрия
§ 30. Построить квадрат по данной его диагонали АВ
Через середину АВ (рис.1) проводим к АВ перпендикуляр MN (см. п. §2). От точки О его пересечения с АВ откладываем на MN отрезки ОС и OD, равные ОА; соединяем точки С и D с точками А и В; ABCD – искомый квадрат.
рис.1
§ 29. Построить квадрат по данной стороне
§ 28. Построить прямоугольник по данным сторонам
Поступает, как в предыдущей задаче; прямой угол α строим, как в §5
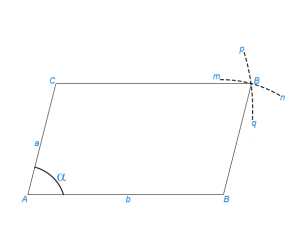
§ 27. Построить параллелограмм по данным сторонам a и b и одному из углов α
Строим ∠ А=α (см. §7); на его сторонах откладываем отрезки АС=а, АВ=b (рис.1). Проводим из В дугу mn радиусом а и из С – дугу pq радиусом b. Точку пересечения этих дуг D соединяем с С и В.
рис.1
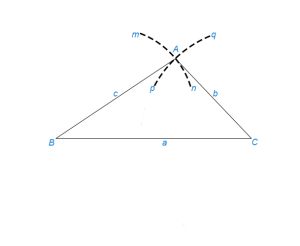
§ 26. Построить треугольник по трем сторонам а, b, с
Пусть наибольшую длину имеет отрезок а. Если а<b+c, то искомый треугольник можно построить так: откладываем отрезок ВС=а (рис.1). Из концов В и С описываем дуги mn и pq радиусами с и b соответственно. Точку пересечения дуг А соединяем с В и С. Если a>b+c, то задача не имеет решения. В промежуточном случае а=b+c условию отвечает только “вырожденный треугольник” – все его вершины лежат на одной прямой.
рис.1
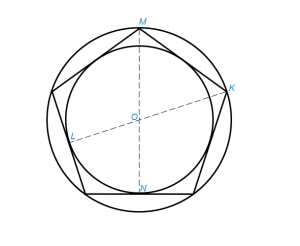
§ 25. Вписать окружность в данный правильный многоугольник
Центр окружности находится, как в предыдущем параграфе §24. Из центра опускаем перпендикуляр ON на одну из сторон (рис.1). Радиусом ON (или OL, рис.2) описываем окружность.
рис.1
рис.2
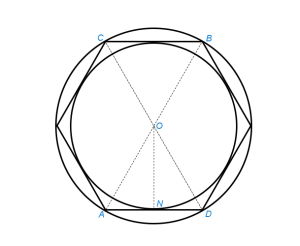
§ 24. Описать окружность около данного правильного многоугольника
Если число сторон четно (рис.1), соединяем прямыми АВ и CD две любые пары противоположных вершин. Из точки их пересечения О радиусом ОА описываем окружность.
рис.1
Если число сторон нечетно (рис.2), опускаем из двух любых вершин К и М перпендикулярны KL и MN на противоположные стороны. Из точки их пересечения О радиусом ОК описываем окружность.
рис.2
§ 23. Вписать окружность в ромб (или квадрат) ABCD
Из точки О пересечения диагоналей проводим ОЕ ⊥ АВ (рис.1). Окружность с центром О и радиусом ОЕ – искомая.
рис.1
В неравносторонний параллелограмм вписать окружность нельзя.
§ 22. Описать окружность около данного прямоугольника (квадрата) ABCD
Проводим диагонали BD и AC (рис.1). Из точки О их пересечения проводим окружность радиусом ОА.
рис.1
Около косоугольного параллелограмма описать окружность нельзя.